Как найти площадь ромба. Как найти площадь ромба Площадь ромба по стороне

Площадь геометрической фигуры - численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
   Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
   
2. Формула площади треугольника по трем сторонам и радиусу описанной окружности
   
3. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
   Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
   
где S - площадь треугольника,
- длины сторон треугольника,
- высота треугольника,
- угол между сторонами и,
- радиус вписанной окружности,
R - радиус описанной окружности,

Формулы площади квадрата

1. Формула площади квадрата по длине стороны
   Площадь квадрата равна квадрату длины его стороны.
2. Формула площади квадрата по длине диагонали
   Площадь квадрата равна половине квадрата длины его диагонали.
   

   S =	1	2
   	2

где S - Площадь квадрата,
- длина стороны квадрата,
- длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

где S - Площадь прямоугольника,
- длины сторон прямоугольника.

Формулы площади параллелограмма

1. Формула площади параллелограмма по длине стороны и высоте
   Площадь параллелограмма
2. Формула площади параллелограмма по двум сторонам и углу между ними
   Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
   

   a · b · sin α

где S - Площадь параллелограмма,
- длины сторон параллелограмма,
- длина высоты параллелограмма,
- угол между сторонами параллелограмма.

Формулы площади ромба

1. Формула площади ромба по длине стороны и высоте
   Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
2. Формула площади ромба по длине стороны и углу
   Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
3. Формула площади ромба по длинам его диагоналей
   Площадь ромба равна половине произведению длин его диагоналей.
где S - Площадь ромба,
- длина стороны ромба,
- длина высоты ромба,
- угол между сторонами ромба,
1 , 2 - длины диагоналей.

Формулы площади трапеции

1. Формула Герона для трапеции

   Где S - Площадь трапеции,
   - длины основ трапеции,
   - длины боковых сторон трапеции,
   

– это параллелограмм , у которого все стороны равны, то для него действуют все те же формулы, как и для параллелограмма, включая формулу нахождения площади через произведение высоты и стороны .

Площадь ромба можно найти, также зная его диагонали . Диагонали делят ромб на четыре абсолютно одинаковых прямоугольных треугольника . Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).

Если в распоряжении только угол и сторона , то можно вооружиться диагональю в качестве помощника и начертить ее напротив известного угла. Тогда она разделит ромб на два конгруэнтных треугольника, площади которых в сумме дадут нам площадь ромба. Площадь каждого из треугольников будет равна половине произведения квадрата стороны на синус известного угла, как площадь равнобедренного треугольника . Поскольку таких треугольников два, то коэффициенты сокращаются, оставив только сторону во второй степени и синус:

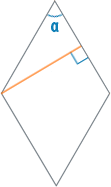
Если внутри ромба вписать окружность , то его радиус будет относиться к стороне под углом 90° , что значит, что удвоенный радиус будет равен высоте ромба . Подставив вместо высоты h=2r в предыдущую формулу, получим площадь S=ha=2ra

Если же вместе с радиусом вписанной окружности, дана не сторона, а угол, то следует сначала найти сторону, проведя высоту таким образом, чтобы получить прямоугольный треугольник с заданным углом. Тогда сторона a может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит

В статье рассмотрим формулу площади ромба и не одну! На картинках покажем, как легко находиться площадь ромба по простым формулам .

Существует большое количество заданий на нахождение той или иной величины в ромбе и в этом нам помогут формулы, о которых и пойдет речь.
Ромб относится к отдельному виду четырехугольников, так как у него все стороны равны. Так же представляет частный случай параллелограмма в котором стороны АВ=ВС=СD=АD равны.

Заметка: Если Вам нужна курсовая, контрольная или дипломная работа, тогда вам на webmath.ru. или просто перейдите по ссылке заказать курсовую работу (http://www.webmath.ru/zakaz_kursovye.php).

Ромб обладает следующими свойствами:

У ромба параллельные углы равные,
- сложение двух соседних углов равно 180 градусам,
- Пересечение диагоналей под углом в 90 градусов,
- Биссектрисами ромба, приходятся его же диагонали,
- Диагональ при пересечении делится на равные части.

Ромб обладает следующими признаками:

Если у параллелограмма в котором диагонали встречаются под углом 90 градусов, то он называется ромбом.
- Если у параллелограмма в котором биссектриса это диагональ, то он называется ромбом.
- Если у параллелограмма равные стороны - это ромб.
- Если у четырехугольника равные стороны - это ромб.
- Если у четырехугольника в котором биссектриса это диагональ и диагонали встречаются под углом 90 градусов, то это ромб.
- Если у параллелограмма одинаковые высоты - это ромб.

Из вышеперечисленных признаков можно сделать вывод, что они нужны для того чтобы научиться отделять ромб от других схожих с ним фигур.

Так как в ромбе все стороны одинаковы периметр находится по следующей формуле:
Р=4а
Площадь ромба формула

Данных формул несколько. Самая простая решается как сложение площадь 2 треугольников, которые получились в результате деления диагоналей.

С помощью второй формулы можно решать задачи с известными диагоналями ромба. В этом случае площадью ромба будет: сумма диагоналей деленная на два.

Очень просто в решении и не забудется.

Третью формулу можно использовать когда знаешь угол между сторон. Зная его можно найти площадь ромба, она будет равна квадрату сторон на синус угла. При чем нет разницы какой угол. так как синус угла имеет единое значение.

Важно помнить что измерение площади происходит в квадратах, а периметра в единицах. Данные формулы очень легко применяются на практике.

Так же могут встретиться задачи на поиск радиуса по вписанной в ромб окружности.

Для этого так же существует несколько формул:

В помощью первой формулы радиус находится как произведение диагоналей поделенное на число полученное от сложения всех сторон. либо равняется половине высоты (r=h/2).

Во второй формуле взят принцип из первой, применяется мы знаем диагонали и стороны ромба.

В третьей формуле радиус выходит из высоты меньшего из треугольников, получившегося в результате пересечения.

– это параллелограмм, у которого все стороны равны.

Ромб с прямыми углами называется квадратом и считается частным случаем ромба. Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.

Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.

Площадь ромба через диагонали

Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.

Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.

Рассмотрим пример расчета площади ромба через диагонали. Пусть дан ромб с диагоналями
d1 =5 см и d2 =4. Найдем площадь.

Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:

Пример расчета площади ромба через стороны также весьма прост. Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .

Площади ромба через сторону и угол

Формула площади ромба через сторону и угол используется очень часто.

Рассмотрим пример расчета площади ромба через сторону и угол.

Задача: Дан ромб, диагонали которого равны d1 =4 см,d2 =6 см. Острый угол равен α = 30°. Найдите площадь фигуры через сторону и угол.
Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
Подставим значения:
Теперь мы знаем сторону и угол. Найдем площадь:

Ромб (с древнегреческого ῥόμβος и с латинского rombus «бубен») является параллелограммом, для которого характерно наличие одинаковых по длине сторон. В случае, когда углы составляют 90 градусов (или прямой угол), такую геометрическую фигуру называют квадратом. Ромб - геометрическая фигура, разновидность четырехугольников. Может быть и квадратом, и параллелограммом.

Происхождение данного термина

Поговорим немного об истории данной фигуры, что поможет немного раскрыть для себя загадочные тайны древнего мира. Привычное для нас слово, часто встречающееся в школьной литературе, «ромб», берет свое начало от древнегреческого слова «бубен». В Древней Греции эти музыкальные инструменты производились в форме ромба или квадрата (в отличие от современных приспособлений). Наверняка вы заметили, что карточная масть - бубна - обладает ромбической формой. Формирование этой масти восходит к тем временам, когда круглые бубны не использовались в обиходе. Следовательно, ромб - древнейшая историческая фигура, которая была изобретена человечеством задолго до появления колеса.

Впервые такое слово, как «ромб» было употреблено столь известными личностями, как Герон и Папа Александрийский.

Свойства ромба

1. Так как стороны ромба противолежат друг другу и являются попарно параллельными, то ромб, несомненно, параллелограмм (АВ || CD, AD || ВС).
2. Ромбические диагонали имеют пересечение под прямым углом (AC ⊥ BD), а, значит, перпендикулярны. Следовательно, пересечение делит диагонали пополам.
3. Биссектрисами ромбических углов являются диагонали ромба(∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
4. Из тождества параллелограммов следует, что сумма всех квадратов диагоналей ромба составляет число квадрата стороны, которое умножили на 4.

Признаки ромба

Ромб в тех случаях является параллелограммом, когда отвечает следующим условиям:

1. Все стороны параллелограмма равны.
2. Диагонали ромба пересекает прямой угол, то есть они перпендикулярны по отношению друг к другу (AC⊥BD). Это доказывает правило трех сторон (стороны равны и находятся под углом в 90 градусов).
3. Диагонали параллелограмма разделяют углы поровну, так как стороны являются равными.

Площадь ромба

1. Площадь ромба равна числу, которое является половиной произведения всех его диагоналей.
2. Так как ромб - это своеобразный параллелограмм, то площадь ромба (S) является числом произведения стороны параллелограмма на его высоту (h).
3. Кроме того, площадь ромба может быть вычислена по формуле, являющейся произведением возведенной в квадрат стороны ромба на синус угла. Синус угла - альфа - угол, находящийся между сторонами исходного ромба.
4. Вполне приемлемой для верного решения считается формула, которая является произведением удвоенного угла альфа и радиуса вписанной окружности (r).